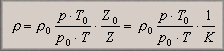Áramlásmérésről alapfokon 2. rész

Áramló folyadékok mennyiségének mérése

Az áramló közegek mérései közül a folyadékok mérésére jöttek létre a legrégebbi technikák. Ókori tárgyi és írásos leletek bizonyítják, hogy a nyitott és zárt csatornákban már egészen szellemes eszközökkel mérték a víz hozamát. Érdemes először a folyadék halmazállapotának korszerű meghatározását felidéznünk: folyadékállapotnak tekintjük azt az anyagállapotot, amelyben az alkotórészek mozgási energiája nagyobb, mint a részecskék közötti kötési energia, de kisebb, mint a molekulák közötti kohéziós erők energiája. Természetesen igaz a hagyományos és szemléletes leírás is, miszerint az a folyadék, amely úgy tölti ki az őt befogadó edényt, hogy annak alakját torzítatlanul felveszi. Reynolds-szám

A mozgó folyadékok áramlástani viselkedésének és hasonlóságának leírására szolgáló, általánosan érvényes összefüggést Osborne Reynolds angol fizikus (1842-1912) állította fel. Az ő nevét viseli az úgynevezett Reynolds szám, amely mindmáig a legfontosabb jellemzője a csőben mozgó anyagok kinematikai viselkedésének. A Reynolds szám az áramló anyagban fellépő tehetetlenségi erők és belső súrlódási erők hányadosa:

Lamináris vagy turbulens?

Fontos megkülönböztetnünk a lamináris és turbulens áramlást. Lamináris az áramlás akkor, ha a közegben a súrlódási erők nagyobbak a tehetetlenségi erőkhöz képest, - ilyenkor az áramvonalak egymás mellett, rétegesen futnak a csőtengellyel párhuzamosan. Turbulens az áramlás akkor, ha az áramló anyagban a tehetetlenségi erők nagyobbak, mint a súrlódási erők, ilyenkor az áramvonalak teljesen szabálytalanul egymásba fonódnak. Az ipari gyakorlatban csaknem kizárólag turbulens áramlásokat kell mérni. A turbulens áramlási tartományt jól jellemzi a Reynolds szám értéke: turbulensnek mondjuk az áramlást, ha a ReDkisebb mint 4000. Általában ez az érték szabja meg az áramlásmérő eszközök alkalmazhatóságának alsó határát.

Mivel mérjünk folyadékot?

A folyadékok térfogatáramának vagy tömegáramának méréssel és számításokkal való meghatározása sokkal egyszerűbb mint a gázoké vagy gőzöké, mert a gyakorlatban a folyadékok összenyomhatatlan anyagként kezelhetők, sűrűségük és viszkozitásuk csak a hőmérséklettől függ. A mérőrendszerek tervezésekor és a mérőeszközök kiválasztásakor fontos szempont a várható áramlási sebességhatárok ismerete. A legkisebb mérhető sebesség a műszer "megszólalási" küszöbértékéről és a minimálisan szükséges Reynolds szám értékétől függ, a legnagyobb sebességet a mérőeszköz konstrukciós adatai és a kavitációs határ szabja meg. Folyadékot a 2. részben felsorolt csaknem minden áramlásmérő eszközzel jól lehet mérni, kivéve természetesen a kifejezetten gázokra kifejlesztett műszereket. - A lamináris tartományba tartozó igen kicsiny anyagáramok mérésére a hidraulikus Ohm törvény alkalmazásán vagy termometriás elven alapuló speciális mérőeszközöket szoktak használni. - A legnagyobb múltjuk a térfogatkiszorításos mérőknek van, pontosságuk és megbízhatóságuk okán ezek nagyon elterjedtek és népszerűek. - Az áramlási sebességet mérő eszközök közül mindegyik alkalmas folyadékok mérésére. Ezek közül, mint korszerű és legjobban fejlődő műszercsaládokat kiemeljük az elektromágneses átfolyásmérőket és az ultrahangos mennyiségmérőket. Az elektromágneses mérőket már igen kis vezetőképességű folyadékok mérésére, imponálóan széles méretválasztékban (DN5...DN3000) gyárt a műszeripar. A műszerekkel akár 100-szoros átfogás is megvalósítható. Tipikus pontosság: 0,5 %. Az ultrahangos áramlásmérők ma még elég drágák, de egyre pontosabb és megbízhatóbb gyártmányok jelennek meg a piacon. Ezekkel is elérhető az 50- 100-szoros átfogás. Jellemző pontosságuk: 0,75-1 % (több sugárutas készülékkel elérhető a 0,25 % !) Alkalmazási előnyök: Sem az elektromágneses, sem az ultrahangos mérő nem okoz áramlási (nyomás) veszteséget a csővezetékben. Mindkét műszerfajta alkalmas kétirányú mérésre is. Alkalmazási hőmérséklethatáruk: +250oC.

Számítómű

A folyadékáramlást mérő rendszerekben nem szükséges bonyolult hozamszámító készülék (Flow Computer) alkalmazása. Sokszor csak egyszerű összegzőművel, igényesebb esetekben hőmérséklet-korrekciós taggal kiegészítve dolgozzák fel a közvetlen áramlásmérő térfogatáram-arányos jelét. Kritikus technológiai mérésekhez, elszámolási alapmérésekhez valamint többfázisú folyadékok (pl. olaj-víz keverék) méréséhez természetesen korszerű, intelligens hozamszámító készülékek szükségesek.

Áramló gázok mennyiségének mérése

Ez a mérési terület igényli a legtöbb fizikai-kémiai megfontolást, rész-mérést és a legnagyobb eszköztárat is. Ez a gáznemű anyagok mechanikai, kinematikai viselkedéséből, és a leírásukra rendelkezésre álló matematikai eljárások viszonylagos bonyolultságából következik. Az ideális gázokra érvényes a Boyle-Mariotte törvény, a valós gázok megközelítőleg pontos leírását pedig 1873 óta ismerjük, amikor - a jobboldali képünkön látható - Nobel-díjas tudós, Van der Waals (1837-1923) publikálta egyenleteit. A számítások finomítása, továbbfejlesztése az un. viriál egyenletek kidolgozásához vezetett az 1930-as években. A közelítések tökéletesítése, a leírás finomítása ma is folyik. Gáznak tekintjük azt az anyagot, amelyben a molekulák mozgási energiája nagyobb, mint a belső kötési energia, és a kohéziós erők elhanyagolhatóak. Az ilyen anyagok hőmérséklete a kritikus hőmérsékletnél nagyobb, azaz hiába nyomjuk össze, soha nem lesz belőlük folyadék. Az alapvető gáztörvények részletezése nélkül induljunk ki abból, hogy a gázok nyomás- és hőmérsékletfüggő sűrűségét a következő összefüggés írja le:

Az egyenletben szereplő tényezők jelentése:

Az áramlástani számításokban általánosan használatos jellemző az anyagok sűrűsége, ezért lényeges a fenti egyenlet ismerete és megoldásának beépítése a korszerű hozamszámító készülékekbe (Flow Computer-ekbe). Róo, Zo értékei a gáz molekuláris összetételétől és a választott normál állapot rögzített adataitól függnek. Z (és így K) értéke minden egyes gáz és gázkeverék esetében más-más módon függ a nyomás és hőmérséklet változásától. Ez az alapja annak, hogy igen pontos gázmennyiség-mérést csak úgy valósíthatunk meg, ha az ismert összetételű gáznak a nyomását és hőmérsékletét is folyamatosan mérjük és ezekből számítjuk a tényleges sűrűséget. Szabványok Ezeket a számítási eljárásokat és az ajánlott algoritmusokat az ISO 12213-1,-2,-3 valamint az ebben hivatkozott ISO 6976 és (MSZ) ISO 13443 dokumentumok tartalmazzák. Ezek magukban foglalják az AGA 8-92DC és a GERG-88 ajánlásokat is, amelyeket ezen az önálló néven is ismer a szakirodalom. Egyszerűbb esetekben, kis nyomásokon és az átlagos környezeti hőmérsékleteken a gázokat ideálisnak is vehetjük, ami azt jelenti, hogy a fenti egyenletekben K=1, és ezzel a klasszikus Boyle-Mariotte törvény alakjához jutunk. Egyéb áramlástani vonatkozásban a gázok mérésekor is érvényesek a folyadékok fejezetben (3. rész) tett általános megállapítások. Itt is ugyanaz pl. a Reynolds szám jelentése és szerepe, mint a folyadékok esetében.

Mérőműszerek

Az áramlásmérő eszközök működésének alapját ugyanúgy a Bernoulli és kontinuitási egyenletek, illetve egyéb mechanikai és termodinamikai törvények képezik és határozzák meg.

Klasszikus gázmennyiség-mérő eszközök:

• a membrános gázmérő ("gázóra")
• a forgódugattyús térfogatszámláló
• a mérőperem, a mérőtorok és a Venturi csöves mérő
• a torlócsöves szondák (átlagoló Pitot-cső)
• a turbinás gázmérők
• a rotaméter

Újabb, korszerű eszközök ( kb. 1985-től):

• az örvényleválásos (Vortex) mérő
• az ultrahangos gázáramlás-mérő (Ultrasonic Flow Meter= UFM)
• a hőelvonásos (termál-diszperziós) tömegárammérő
• a Coriolis erőt használó tömegárammérő

Természetesen vannak a fentieken kívül egyéb, rendkívül bonyolult vagy éppen primitíven egyszerű áramlásjelző, -mérő eszközök is, hiszen a gázmérés piaca mind igény, mind kínálat szempontjából szinte áttekinthetetlenül nagy. Hozam-számítómű A korszerű - főleg az elszámolás alapját képező - mérőrendszerek elengedhetetlen része az intelligens hozam-számítómű (flow computer), amelynek egyik legfontosabb feladata a fent érintett sűrűségszámítás elvégzése minden időpillanatban. Gázkeverékek (pl. földgáz) esetében, amikor akár 10-15 komponens mol%-ának folyamatos változásával kell számolnunk, igen intelligens készülékre van szükségünk ha az alapvető átfolyási egyenleteken kívül a már említett viriál egyenleteket megoldva, a kompresszibilitás mindenkori értékét is elfogadható pontossággal akarjuk meghatározni. Pontosság A legkorszerűbb gázmennyiség mérőállomásokon ma már a 0,75...1,25%-os eredő térfogatáram-mérési- és 1,5...2,5%-os tömegáram-mérési bizonytalanság érhető el. Erre a pontosságra tartós üzemben elsősorban a mérőperemes és az UFM rendszerek képesek. Sokan esküsznek aturbinás mérőkre is, hiszen a világ nagy gázmérő hálózatainak 20-25 %-a használ turbinákat. Amennyiben a gáz nem túl szennyezett és a mérőállomás gépészeti, hidromechanikai kialakítása ezt lehetővé tesz, továbbá igen fejlett az üzemeltetési és karbantartási kultúra, akkor a mai turbinákkal is igen jó eredmények érhetőek el. A turbinagyártók katalógusaiban újabban találunk olyan specifikációt, amely 0,15...0,25%-os pontosságot ígér. Ilyenkor mindig figyelembe kell venni, hogy az ilyen turbinával megvalósított teljes mérőrendszer térfogatáramra vonatkoztatott eredő bizonytalansága a valóságban legjobb esetben is 1...1,5% lehet ! Hőteljesítmény és hőmennyiség mérése Az áramlásmérés egyik gyakori célja a folyadékok és gőzök által szállított hőmennyiség mérése. A hőszállító és hőközlő anyag az ipari gyakorlatban csaknem kizárólag a víz és a vízgőz. A hőteljesítményt a tömegáram és a fajlagos entalpia pillanatértékeinek szorzataként határozhatjuk meg, a szállított hőmennyiséget pedig a hőteljesítmény időbeli integrálásával (folyamatos összegzésével) kapjuk. A mérőrendszer két , jól megkülönböztethető részből áll:

• folyamatos tömegáram-mérésből és
• folyamatos hőmérséklet(különbség) -mérésből

A tömegáram-méréssel az előző részekben már foglalkoztunk. Itt csupán azt kívánjuk hangsúlyozni, hogy minden egyes feladat esetében tudni kell, hogy az alkalmazott primer jelképző és távadó eszköz térfogat- vagy tömegáramot mér. A térfogatáramot minden esetben át kell számítani tömegárammá ahhoz, hogy a hőteljesítményhez, mint mérendő részadathoz jussunk! A hőmérsékletmérés A hőmérsékletnek a hőmennyiségmérésben kettőzött szerepe van, mert egyrészt a tömegáram meghatározásában, másrészt az entalpia (belső energiatartalom) számításában van szükség az abszolút hőmérséklet Kelvinben kifejezett értékére. Ezért az alkalmazott hőmérséklet érzékelők (távadók) valamint az egész hőmérsékletmérő kör pontossága nagyon érzékenyen befolyásolja a hőmennyiség-mérés eredő pontosságát. Különösen a hőmennyiség-különbség közvetlen mérőköreiben fontos az "előremenő" és a "visszatérő" ágak hőmérsékletének lehető legpontosabb mérése. Ezt a hőmérő pár együttfutásának biztosításával, (válogatással, többpontos kalibrálással) valamint gondos beépítéssel és hatásos hőszigeteléssel kell biztosítani. Ipari körülmények között azonban a legszerencsésebb esetben sem lehet ezen értékeket 0,25 K-nél kisebb hibával meghatározni, a biztonságosan mérhető Dt pedig 1 K-nél nem lehet kevesebb! A víz és egyéb folyadék Az itt használt hőmennyiség-mérők legtöbbször a következő, egyszerű összefüggést használják: Q = qm * c * delta t ahol Q = hőteljesítmény, qm= tömegáram, c= fajlagos hőkapacitás és delta t= a hőmérséklet-különbség. A "c" értékét egyszerűbb esetben egyetlen állandóval, vagy (komolyabb méréseknél) hőmérsékletfüggő táblázatos adatokkal veszik figyelembe, attól függően, hogy mekkora a pontossági igény. Így működnek a háztartási vagy kisüzemi (kompakt) melegvizes hőmennyiség-mérők is, amelyek általában egy forgóelemes térfogatáram-mérőből és egy hőmérő-párból állnak. Vízgőz A vízgőz hőmennyiségének mérésekor jóval bonyolultabb számításokat kell végrehajtani. Szükség van a fajtérfogat és fajlagos entalpia folyamatos és egyidejű számítására. A számításokat a mindenkori nyomás- és hőmérsékletértékekből, valamint a tömegsebességre jellemző mennyiségi jelből, a kritikus nyomás- és hőmérséklet-értékek és egyéb termodinamikai állandók felhasználásával tudjuk elvégezni. Ezekhez a műveletekhez mindig intelligens hozamszámító eszközökre van szükség. Mivel mérjük? A primer mérőeszközök közül a következők használata a legelterjedtebb:

• Szárnykerekes melegvízmérők (kisüzemi kompakt eszközök)
• Turbinás mérővel működő rendszerek - csak vízre!
• Elektromágneses áramlásmérő/távadók - csak vízre!
• Mérőperemes jelképzők dp/i távadókkal - vízre és vízgőzre
• Ultrahangos mennyiségmérők - csak vízre!

Természetesen minden tömegáram-mérővel lehet hőmennyiségmérő kört építeni. Mindezek alapján azt lehet mondani, hogy a tömegárammérés hibahatárait is figyelembe véve, a különféle mérési módszerekre a következő eredő mérési bizonytalanságok a jellemzők (a +30oC ... +150oC tipikus tartományban):

• kisüzemi kompakt hőfogyasztásmérők: 3 %
• turbinás mérőrendszerek: (1,5...1,75) %
• mérőperemes mérőkörök: (0,9...1,25) %
• elektromágneses mérővel működő mérések: (0,75...1) %
• ultrahangos mérőrendszerek: ( 0,6...1,1) %

A korszerű hőteljesítmény- és hőmennyiség-mérő rendszereknek fentiek miatt elengedhetetlen része az összetett és folyamatos termodinamikai számítási algoritmus. Elszámolási mérés esetében garantálni kell az algoritmus (és a mérőberendezés) megváltoztathatatlanságát és OMH hitelesíthetőségét. Ez legkönnyebben kompakt, intelligens hozamszámító készülékekkel valósítható meg.